Les microcontrôleurs Arduino sont très abordables et permettent de réaliser une infinité de projets grâce aux capteurs et actionneurs compatibles, disponibles sur le marché.
La communauté open source associée en fait l’une des plateformes les plus faciles à mettre en œuvre et à utiliser avec un minimum de connaissances en électronique.
Tout système automatique repose sur trois composantes :
- Un contrôleur capable de recevoir des informations, de faire des calculs, de mettre en œuvre une logique et d’en déduire une série d’actions à réaliser. (Ordinateur, automate, microcontrôleur)
- Un capteur : Organe permettant de mesurer, de détecter… Il apporte de l’information depuis le milieu extérieur au contrôleur. (Capteur de température, interrupteur, accéléromètre, GPS…)
- Un actionneur : Organe permettant au système d’agir sur son environnement. (Moteur, vanne, pompe…)
Généralement, il est nécessaire de supprimer des valeurs aberrantes et un bruit de mesure haute fréquence. Tout cela doit être réalisé en restant fidèle à la mesure, en détériorant le moins possible de signal brut.
Cet article propose 2 méthodes de filtrage numérique à la fois simples et performantes avec des applications à Arduino.
Les équations présentées ne sont pas basées sur des modèles physiques prédictifs et peuvent donc être appliquées à n’importe quel type de capteur. C’est un outil puissant.
Méthode 1 : Modération de la mesure par la valeur filtrée précédente (coef K)
Le signal filtré à l’instant N est égal au signal filtré à l’instant N-1 corrigé d’une fraction K de l’écart entre la mesure à l’instant N et le signal filtré de l’instant N-1.
L’équation mathématiques correspondante est donc :
$ F(N) = F(N-1) + [ M(N) – F(N-1) ] . K $
Avec 0<$K$<1
$F$ le signal filtré
$M$ la mesure brute
Cette équation peut être ré-arrangée ainsi :
$ F(N) = (1-K) . F(N-1) + K . M(N) $
Cette équation est en deux parties distinctes. Selon la valeur de $K$, la valeur filtrée $F(N)$ prend plus ou moins en compte la nouvelle mesure $M(N)$.
Dans ce tableau on voit que pour différentes valeurs de $K$, la nouvelle mesure se voit attribuer une pondération opposée à celle attribuée à la valeur précédemment obtenue.
$K$ est le coefficient permettant de pondérer la prise en compte de la nouvelle mesure par rapport à la valeur obtenue précédemment.
$K$ représente donc la quote-part de la mesure au temps $N$ par rapport à la valeur filtrée obtenue au temps $N-1$.
Prenons maintenant un exemple visuel. Sur le graphique suivant, un signal brut est présenté en fonction du temps.
Deux parties distinctes sont identifiables.
- Pour un temps compris entre 0 et 120 unités de temps, le signal ressemble à ce que pourrait produire un capteur.
- Il y a par exemple deux valeurs aberrantes, l’une au temps 6 et l’autre au temps 41. Ces valeurs aberrantes peuvent être assimilées à des Dirac.
- Tout au long de ce signal, des perturbations haute fréquence viennent bruiter la mesure.
- Pour un temps supérieur à 120 unités : le signal représente un échelon. Cette portion est intéressante pour étudier le comportement d’un filtre.
A partir de ce signal brut, un signal filtré est calculé en utilisant la formule précédemment citée. Le calcul est réalisé pour différentes valeurs de $K$. Le résultat est présenté sur la figure suivante.
Faibles valeurs de $K$, entre 0 et 0,3 :
- On constate un lissage important effaçant significativement les potentielles valeurs aberrantes.
- En contrepartie, le signal obtenu est beaucoup moins sensible aux variations et il semble prendre du retard. Un déphasage (glissement vers la droite) apparaît.
Valeurs de $K$ autour de 0,5 :
- Sur cet exemple, le signal filtré semble rester fidèle au signal d’origine tout en lissant la courbe.
Grandes valeurs de $K$, de 0,8 à 1 :
- Le lissage est très faible, les aberrations bien que moins significatives sont toujours présentes.
- Le signal filtré reste très fidèle au signal brut. Il est même un peu trop fidèle et lisse trop peu le signal brut.
D’un point de vue visuel, ici, une valeur de $K=0,5$ semble bien adaptée pour le lissage de la courbe. Cependant, dans la pratique, une valeur plus faible peut s’avérer plus pertinente. En effet le déphasage dans le temps n’est pas forcément un problème si la vitesse d’acquisition du capteur est suffisamment importante.
A ce stade, appliquons cette méthode à un cas concret. La capture d’écran ci-dessous représente le filtrage du signal d’un capteur de pression relié à un Arduino Nano. En bleu, le signal numérique brut, lu par l’Arduino. Les 3 autres courbes représentent le signal filtré :
Méthode 2 : Moyenne glissante
Voici une deuxième méthode permettant de filtrer un signal brut. Il s’agit de calculer la moyenne glissante du signal d’entrée sur les « $T$ » dernières valeurs.
L’équation est la suivante :
$ F(N) = \displaystyle\sum_{i=0}^{T-1} \frac{M(N-i) } {T} $
$F$ le signal filtré
$M$ la mesure
$T$ le nombre de mesures prises en compte.
Comme dans la partie précédente, on considère le même signal brut et on lui applique la formule pour observer les effets du filtrage. Cette méthode est appliquée en prenant en compte 5, 10 et 15 valeurs précédentes.
Plus la moyenne prend en compte un grand nombre de valeurs, plus le lissage est important mais plus le phénomène de déphasage se fait ressentir. Là aussi, il y a un optimum à trouver en fonction du système et du résultat souhaité.
La capture d’écran ci-dessous représente le filtrage du signal d’un capteur de pression relié à un Arduino Nano. En bleu, le signal numérique brut, lu par l’Arduino. Les 3 autres courbes représentent le signal filtré :
Astuce : Modération de la mesure en cascade
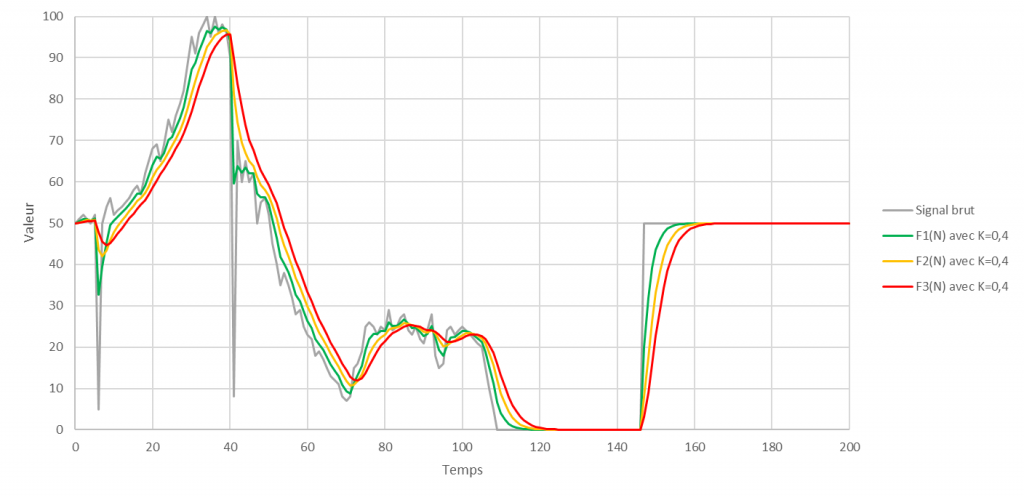
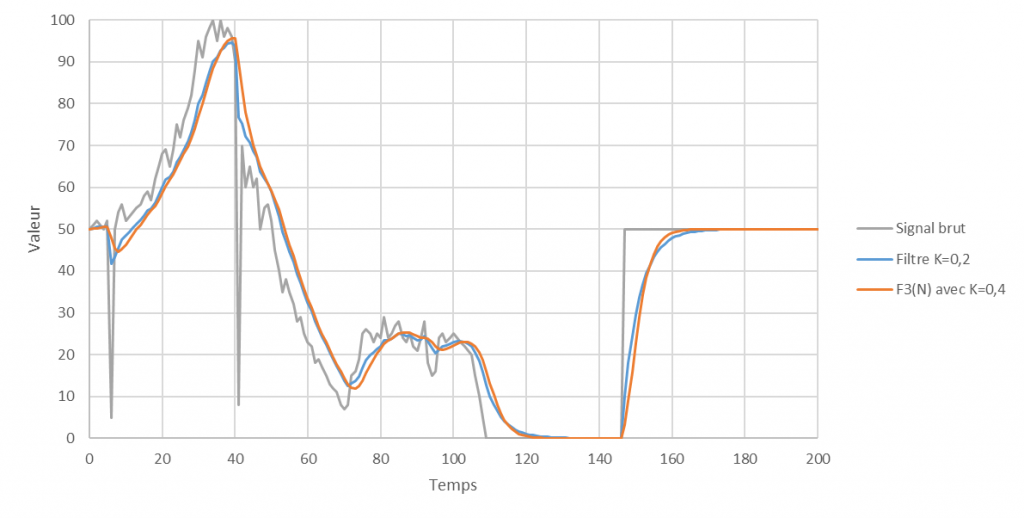
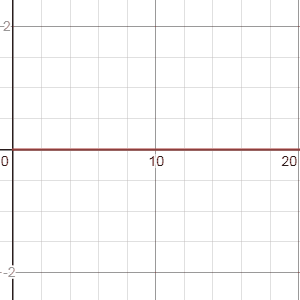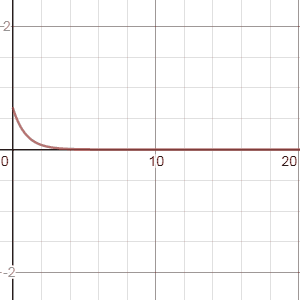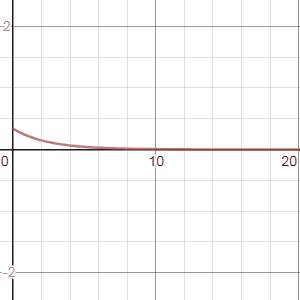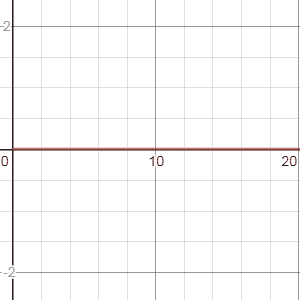Ici, il ne s’agit pas d’une nouvelle méthode mais d’une astuce. Comme avec des circuits électriques RLC, il est possible d’utiliser des combinaisons de filtres en série et en parallèle.
Par exemple, une cascade (enchaînement en série) de filtres, permet d’obtenir des résultats très intéressants.
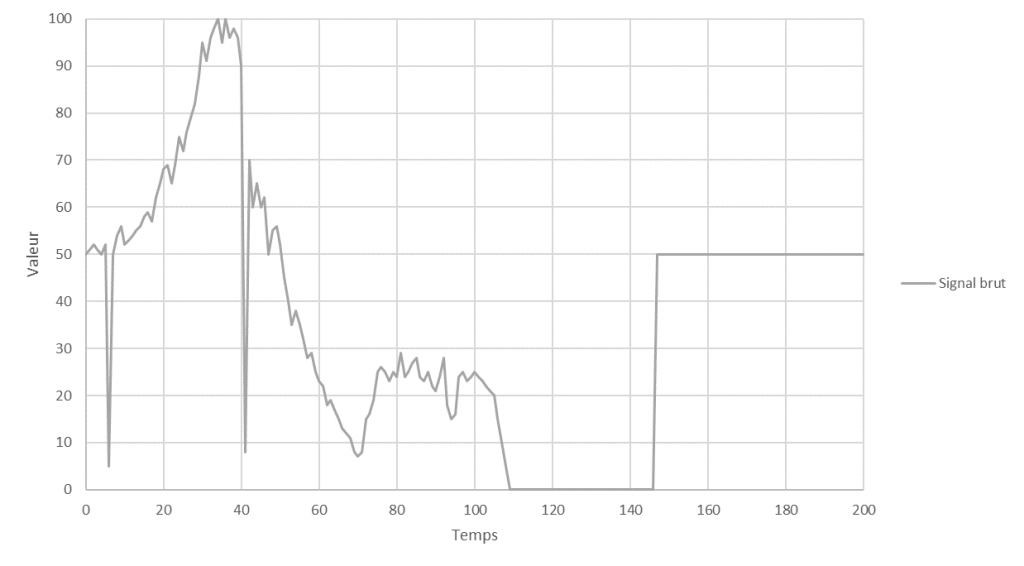
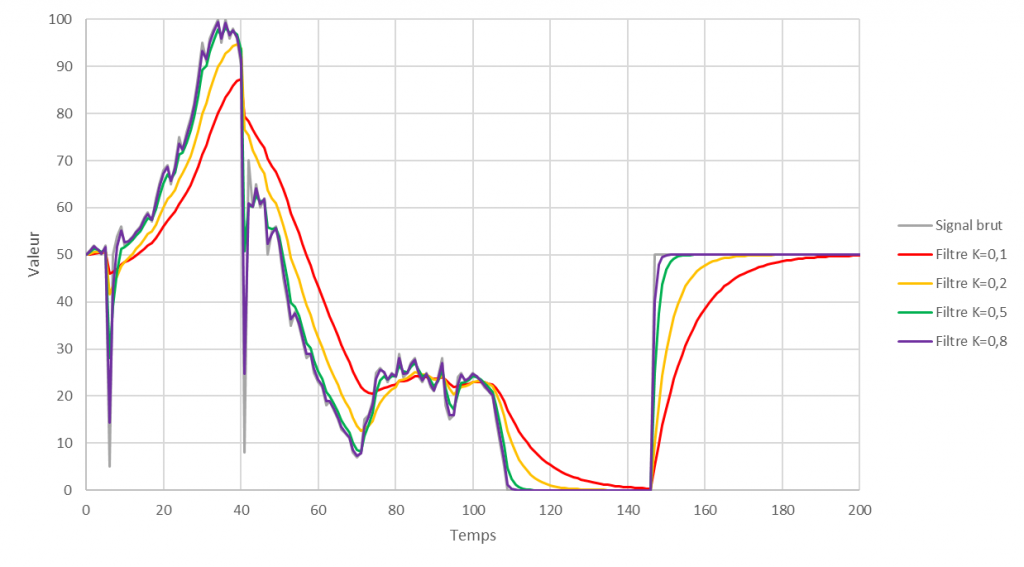
Prenons l’exemple de la première méthode utilisant le coefficient $K$.
En appliquant un premier filtre $F_1$ à la mesure M on obtient :
$ F_1(N) = (1-K) . F_1(N-1) + K . M(N) $
A ce premier résultat, on applique à nouveau le même filtre ($K$ identique pour chaque filtre). On obtient donc le système d’équation :
$ \begin{cases} F_1(N) &= (1-K) . F_1(N-1) + K . M(N) \\ F_2(N) &= (1-K) . F_2(N-1) + K . \textbf{F_1(N)} \end{cases} $
Qui se simplifie en une équation :
$F_2(N) = (1-K) . F_2(N-1) + (K-K²) . F_1(N-1) + K² . M(N)$
Cette équation peut se généraliser à $i$ filtres en cascade :
$F_i(N) = \displaystyle\sum_{j=0}^{i-1} \textcolor{red}{(K^j-K^{j+1}).F_{i-j}(N-1)} + \textcolor{green}{K^i.M(N)}$
Cette dernière équation signifie que, plus le nombre de filtres en série est important (plus $i$ est grand), moins la valeur de la mesure à l’instant $N$ ($\color{green}M(N)$) impacte la valeur filtrée ($F_i(N)$). En effet, pour $0<K<1$, la valeur de $\color{green}K^i$ décroit quand $i$ croit.
Dans la cascade de filtres, le premier filtre a très peu d’impact et le dernier a beaucoup d’impact. Par exemple, pour $ i=3 $:
$F_1(N-1)$ se voit attribué le coefficient $\color{red}{(K^2-K^3)}$
$F_3(N-1)$ se voit attribué le coefficient $\color{red}{(1-K)}$
Et pour toute valeur de $0<K<1$, on a $\color{red}{(K^2-K^3)} < \color{red}{(1-K)}$.
A titre d’exemple, voici le résultat obtenu avec une cascade de filtres ayant tous pour constante $K=0,4$.
Trois filtres en cascade avec un $K=0,4$ permettent d’obtenir un signal très proche d’un simple filtre avec $K=0,2$.
Conclusion
Les différentes courbes tracées dans cet article permettent de visualiser l’impact de différents filtres sur un signal brut. C’est un outil de compréhension permettant d’observer le comportement d’un filtre. Cependant, à chaque application, il faudra se poser la question du comportement souhaité et du besoin du système. Les filtres devront être testés et réglés spécifiquement.
Pour aller plus loin, vous pouvez télécharger le document Excel ayant servi à illustrer cet article.
Si vous connaissez une autre méthode de filtrage, décrivez-la en commentaire pour donner des idées aux autres lecteurs.
Si vous avez apprécié cette lecture, n’hésitez pas à partager cet article avec d’autres personnes qui pourraient être intéressées. C’est un moyen simple de soutenir ce blog.
